1.導入: ポートフォリオ最適化とは
ポートフォリオ最適化は、所与のリスクレベルにおいて最大の期待リターンをもたらす、または所定の期待リターンに対して最小のリスクを持つような資産の組み合わせを求めるプロセスです。このプロセスは、投資家が自身のリスク許容度や投資目的に合わせて最適な投資ポートフォリオを形成するのを助けます。最適化されたポートフォリオは、リスクとリターンのバランスを最大化することが目的です。
ポートフォリオの基本概念
| 概念 | 説明 |
| リターン | 投資の収益率。期待リターンは未来の収益の平均値として予測される。 |
| リスク | 投資の変動性や不確実性を表す。ボラティリティや標準偏差で計測されることが多い。 |
| 投資ユニバース | 投資家が選択できる全ての投資の集合。 |
| 効率的フロンティア | 与えられたリスクレベルでの最大の期待リターン、または与えられた期待リターンでの最小リスクを表すポートフォリオの集合。 |
| マーケットポートフォリオ | 全てのリスク資産を市場価値加重で持つポートフォリオ。 |
| リスクフリーレート | 無リスク資産(通常、短期国債など)の収益率。 |

2.リターンの理解と計算
① 過去のリターンの計算
過去のリターンを計算する際には、指定された期間の初めと終わりの価格、加えてその期間に受け取った配当や利息を考慮します。これにより、その期間の投資の実際の収益率が評価されることになります。
計算式:

この式を用いて、投資の収益率や損益を評価することができます。例として、株式の場合、年初の株価、年末の株価、その年に受け取った配当を使用して年間のリターンを計算することができます。
過去データに基づくリターンの算出例の詳細
| 年度 | 開始価格 | 終了価格 | 配当 | リターン計算 | リターン率 |
| 2021 | ¥10,000 | ¥11,000 | ¥500 | ¥1,500 | 15.00% |
| 2022 | ¥11,000 | ¥10,500 | ¥400 | -¥100 | -0.91% |
| 2023 | ¥10,500 | ¥12,000 | ¥600 | ¥2,100 | 20.00% |
上記の表は、各年度の開始価格、終了価格、配当をもとに、リターンの絶対値を計算したものです。そして、それを開始価格で割ることで、リターン率を算出しています。このような計算を通じて、過去の投資の実績やパフォーマンスを評価することができます。
② 期待リターンの推定
期待リターンとは、将来にわたるある投資の平均的な収益率を指します。期待リターンを推定する方法は複数ありますが、一般的には過去のリターンの平均や、特定のモデルを用いた計算が行われます。また、外部環境の変化や新しい情報に基づく予測を組み入れることも可能です。
計算式:

上記の式は、過去のリターンの算術平均を取る単純な方法を示しています。ただし、この方法だけに頼るのではなく、業界のトレンドや経済的な指標なども考慮に入れることが推奨されます。
期待リターンの計算方法の詳細
| 年度 | 過去のリターン率 |
| 2021 | 15.00% |
| 2022 | -0.91% |
| 2023 | 20.00% |
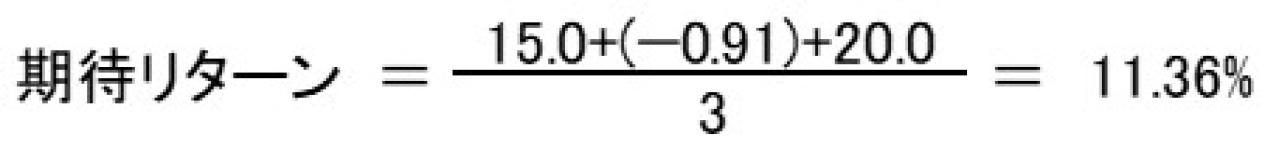
上記の表は、過去3年間のリターン率を示しており、これらの平均値を取ることで期待リターンを計算しています。この例では、過去3年の期待リターンは約11.36%となります。

3.ボラティリティの理解と計算
① ボラティリティの意味
ボラティリティは、資産価格の変動の度合いを示す統計的指標であり、通常、標準偏差や分散として計算されます。株価や金利、商品価格などの金融資産の価格変動の大きさを捉えるのに用います。ボラティリティが高ければ高いほど、その資産の価格変動は大きいとされ、リスクが高いと考えられます。
ボラティリティの計算:
ボラティリティ = 標準偏差(過去のリターン)
リターンの計算:
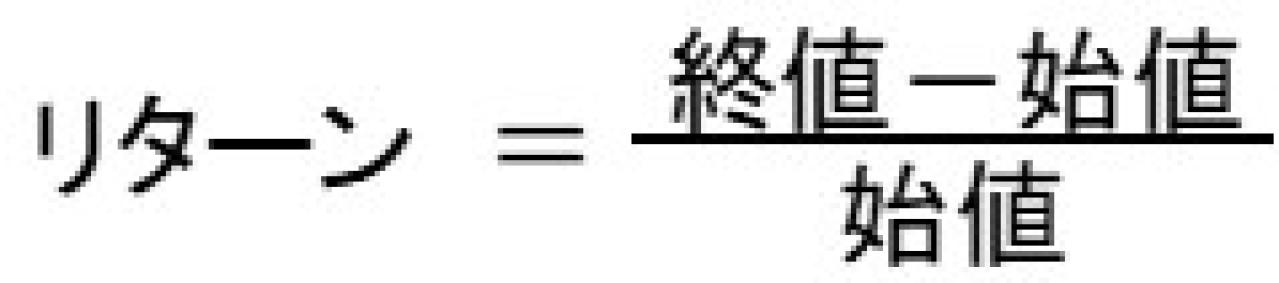
資産のリターンの時間的な変動を示すボラティリティは、将来的な価格変動の予測や、投資ポートフォリオのリスク管理に役立てることができます。
ボラティリティの具体例
| 年/月 | 始値 | 終値 | リターン | ボラティリティ |
| 2023年1月 | ¥100 | ¥105 | 5.00% | - |
| 2023年2月 | ¥105 | ¥103 | -1.90% | - |
| 2023年3月 | ¥103 | ¥110 | 6.80% | - |
表中の「ボラティリティ」の項目は、通常は時系列データの一定期間(例:過去1年間)のリターンの標準偏差として計算されるため、月ごとには示されないことが多いです。この表は、月次リターンの標準偏差を計算する前段階のデータを示しています。
② ヒストリカルボラティリティの算出
ヒストリカルボラティリティ(過去のボラティリティ)は、過去の価格データを用いて算出される資産の変動性の指標です。具体的には、ある期間における過去のリターンの標準偏差として計算されます。ヒストリカルボラティリティは、その資産が過去にどれだけの変動を持っていたかを示すものであり、その資産の将来の変動の大きさを予測するための指標として用いられます。
ヒストリカルボラティリティの計算:
ヒストリカルボラティリティ = 標準偏差(過去n期間のリターン)
ここで、n期間とは、例えば過去20日間や過去1年間など、分析者が選択する期間を指します。
ヒストリカルボラティリティの算出例
| 年/月 | リターン | 累積リターン |
| 2023年1月 | 5.00% | 5.00% |
| 2023年2月 | -1.90% | 3.10% |
| 2023年3月 | 6.80% | 9.90% |
| : | : | : |
| 2023年12月 | 3.50% | x.x% |
ヒストリカルボラティリティ(過去1年間): y.y%
この表は、12ヶ月間の月次リターンを元にヒストリカルボラティリティを計算する例を示しています。具体的なヒストリカルボラティリティの値(y.y%)は、全てのリターンの標準偏差によって得られます。
③ 予測ボラティリティの推定
予測ボラティリティは、未来の資産の価格変動の大きさを予測するためのボラティリティの値です。この予測ボラティリティの推定には、数多くのモデルや手法が存在しますが、中でもGARCHモデルは非常にポピュラーなものの一つとして知られています。
GARCH(Generalized Autoregressive Conditional Heteroskedasticity)モデルは、時間とともに変動するボラティリティをキャッチすることができる統計的モデルです。過去の価格変動(リターンの二乗)から、将来のボラティリティを予測するために使用されます。
GARCHモデルの基本的な考え方は、大きな価格変動が続く時期と小さな価格変動が続く時期があるというものです。このモデルは、過去のリターンの情報だけでなく、過去のボラティリティの情報も取り入れて、ボラティリティの予測を行います。
GARCHモデルによる予測ボラティリティ
| 年/月 | 実際のリターン | GARCHによる ボラティリティ予測 |
| 2023年1月 | 5.00% | 15.20% |
| 2023年2月 | -1.90% | 14.80% |
| 2023年3月 | 6.80% | 16.10% |
| : | : | : |
| 2023年12月 | 3.50% | x.x% |
この表では、各月の実際のリターンに対して、GARCHモデルを用いて予測された翌月のボラティリティが示されています。GARCHモデルは、過去の価格データとボラティリティの情報を元に、未来のボラティリティの予測を行うためのツールとして利用されます。
4.シャープレシオとは
① シャープレシオの定義
シャープレシオは、1966年にWilliam F. Sharpeによって提唱され、投資の効果的なパフォーマンスを評価する指標として広く採用されています。この指標は、リスクとリターンのバランスを示すための数値で、高い値を示す投資は、低いリスクで高いリターンを提供すると解釈されます。
基本的な計算式

計算式の各項目の説明
a.ポートフォリオの収益率
投資対象となるポートフォリオの過去または将来の期待収益率。通常は年率で示される。
b.無リスク金利
通常、国債や短期国債など、リスクが非常に低いとされる金融資産の収益率を使用する。この値は、投資家がリスクを取らずに得られるリターンを示す。
c.ポートフォリオの標準偏差
ポートフォリオのリターンの変動性を示す指標。この値が大きいほど、リターンの変動が大きい、つまりリスクが高いと解釈される。
シャープレシオは、他の多くのリスク調整リターン指標と同様に、リターンだけでなくリスクも考慮して投資のパフォーマンスを評価する際に役立つ指標として用いられます。
② シャープレシオの計算と解釈
シャープレシオは、投資のリスク調整後のパフォーマンスを評価するための指標です。計算において、リターンとリスクのバランスを示すことができるので、異なるポートフォリオや投資戦略の比較に役立ちます。
計算のステップ
・ポートフォリオの平均収益率を計算する。
・無リスク金利を決定する。通常、短期国債などのリスクフリーとされる資産の収益率を使用する。
・ポートフォリオの収益率の標準偏差(ボラティリティ)を計算する。
・上記の数値を利用して、シャープレシオを計算する。
シャープレシオの算出例
| 年度 | ポートフォリオ 収益率 |
無リスク金利 | 標準偏差 | シャープレシオ |
| 2021 | 8% | 2% | 15% | 0.4 |
| 2022 | 10% | 2% | 14% | 0.57 |
| 2023 | 7% | 2% | 16% | 0.31 |
解釈のポイント
a.シャープレシオが高いほど、単位リスク当たりの収益が高いとされます。これは、同じリスクを取る中でより高い収益を得る投資戦略やポートフォリオであることを示します。
b.逆に、シャープレシオが低い場合、その投資は単位リスク当たりの収益が低いと解釈されることが多いです。
c.異なる投資戦略や資産クラス間での比較にも使えますが、同じ市場やカテゴリ内での比較が最も意味を持ちます。
シャープレシオは非常に便利な指標ですが、他の多くの指標と同様に、単独での評価だけに依存するのではなく、他の情報や指標と合わせて考慮することが重要です。

5.効果的なポートフォリオの組み合わせ
① 効率的フロンティアとは
効率的フロンティアは、モダン・ポートフォリオ理論の中心的なコンセプトとして知られています。ハリー・マーコウィッツによって1950年代に導入されたこの理論は、投資家が最大のリターンを追求しつつリスクを最小化する方法を探求します。
a.基本的な考え方
効率的フロンティアは、与えられたリスクレベルに対して最も高いリターンを提供する投資ポートフォリオの集合、または与えられたリターンに対して最も低いリスクを持つポートフォリオの集合を示します。
b.リスクとリターン
ここでの「リスク」とは、通常、ポートフォリオの収益の標準偏差(ボラティリティ)として測定されます。一方、「リターン」は、ポートフォリオの期待収益率として考えられます。
c.グラフの解釈
効率的フロンティアは通常、縦軸に期待リターン、横軸にリスク(ボラティリティ)を取ったグラフ上に描かれます。この曲線の上の各点は、それぞれのリスクレベルでの最適なポートフォリオを示しています。
d.非効率的なポートフォリオ
効率的フロンティアの下側に位置するポートフォリオは「非効率的」と見なされます。これは、同じレベルのリスクでより高いリターンを達成できる効率的なポートフォリオが存在するためです。
e.多様化の重要性
効率的フロンティアは、資産間の相関が完全でない場合にのみ存在します。言い換えれば、資産間の相関が低い(または負)であるために、リスクを分散し、全体のポートフォリオのリスクを低減できることを示しています。
この理論の背景には、個別の投資先のリターンだけでなく、投資先同士の相関関係も重要であるという考え方があります。リスクを最小化しながら期待リターンを最大化するための最適な組み合わせを見つけ出すことが、効率的フロンティアの主な目的です。
② 最適なポートフォリオの選定
最適なポートフォリオの選定とは、投資家のリスク許容度や目標リターンに基づいて、最も適切な資産配分を決定するプロセスを指します。この選定の中心となるのが、シャープレシオです。
a.シャープレシオ
シャープレシオは、超過リターン(投資の収益率と無リスク資産の収益率との差)をリスク(ボラティリティまたは標準偏差)で割ったものです。この値が高ければ高いほど、リスクを取ることに対するリターンの質が良いと評価されます。
b.最適ポートフォリオの特徴
効率的フロンティア上でシャープレシオが最も高いポートフォリオが最適なポートフォリオと見なされます。このポートフォリオは「接触点」または「切片ポートフォリオ」とも呼ばれ、リスクフリーレートから効率的フロンティアに接触する点でのポートフォリオを指します。
c.投資家のリスク許容度
各投資家はリスクを取ることで得られるリターンに対する期待や許容度が異なります。そのため、ある投資家にとっての最適なポートフォリオは、別の投資家にとっては最適でない場合があります。リスク許容度や目標リターンに基づいて、効率的フロンティア上の最適な点を選ぶことが重要です。
d.制約と考慮事項
実際のポートフォリオ最適化では、リスクとリターンだけでなく、流動性、税制、取引コスト、将来の資金需要など、さまざまな制約や考慮事項を取り入れることが多いです。
e.継続的な再評価
最適なポートフォリオは、市場環境や投資家の目標、リスク許容度の変化に応じて時々更新する必要があります。定期的な再評価と調整が、長期的な投資成功の鍵となります。
最適なポートフォリオの選定は、投資の目的、期間、リスク許容度など、投資家個人の状況やニーズに応じて異なります。そのため、このプロセスは一度きりではなく、継続的に見直しを行うことが推奨されます。

6.最適化手法とツール
① ポートフォリオ最適化の数学的手法
ポートフォリオ最適化の数学的手法は、過去のデータや予測に基づいて、最も効果的な資産の組み合わせを求めるためのものです。これには、資産の期待リターン、ボラティリティ(リスク)、相関関係などの要因が関与します。
a.平均分散最適化 (Mean-Variance Optimization)
定義: 投資家が取るリスクを最小限に抑えながら、期待リターンを最大化する資産の組み合わせを見つける手法。
数学的表現:maxwTμ−2λwTΣw
w = 資産の重みベクトル
μ = 期待リターンベクトル
Σ = 共分散行列
λ = リスク回避係数
b.最大化シャープレシオ
定義:ポートフォリオの期待リターンをポートフォリオのボラティリティ(標準偏差)で割った値(シャープレシオ)を最大化することを目的とする最適化手法。
数学的表現:
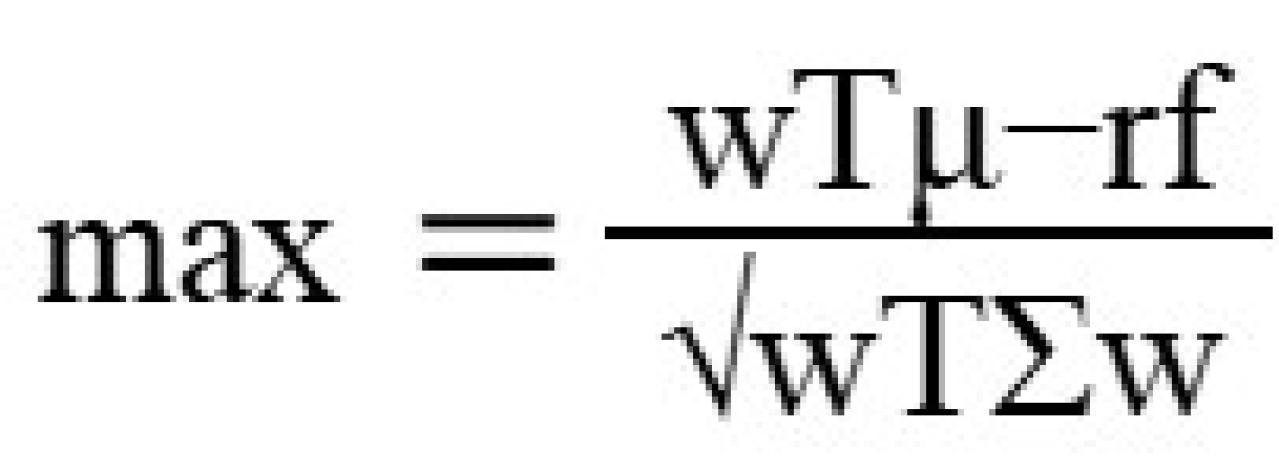
rf = 無リスク金利
上記の他の変数は平均分散最適化の場合と同様です。
これらの数学的手法は、多くの金融エンジニアリングやポートフォリオ管理の文献で詳細に議論されています。
② 実践的な最適化ツールの紹介
投資家やポートフォリオマネージャーは、ポートフォリオ最適化を行う際に、多くの最適化ツールやソフトウェアを使用します。これらのツールは、データの取り扱いや数学的な計算を簡易化し、効果的な結果を迅速に提供します。
a.MSCI Barra
MSCI Barraは、リスクモデリングとポートフォリオ管理のためのソフトウェアとして広く認知されています。多くの投資家が、このツールを使用してポートフォリオのリスクやリターンを分析します。
b.Black-Littermanモデル
このモデルは、主観的な見解や市場均衡を組み込むことで、期待リターンの推定を向上させるためのものです。特に、投資家の独自の見解をポートフォリオ最適化に組み込む場合に使用されます。
c.MATLAB
MATLABは、数学的計算やデータ分析を行うための高度なプログラミング環境です。金融ツールボックスを使用することで、ポートフォリオ最適化のための多くの関数やアルゴリズムが利用できます。
これらのツールやモデルは、投資家のニーズや目的に応じて選択されるべきです。最適なツールを選択することで、ポートフォリオのパフォーマンスやリスク管理が向上します。

7.おわりに:ポートフォリオ最適化の重要性
ポートフォリオ最適化は、資産の選定と配分を行い、期待リターンを最大化し、同時にリスクを最小化するプロセスを指します。この最適化は、金融の世界におけるキーとなるコンセプトであり、投資家が目標とするリターンを得るための助けとなります。
a.リスクとリターンのバランス
投資の世界において、リスクとリターンは密接に関連しています。高いリターンを求める場合、それに伴うリスクも増大します。ポートフォリオ最適化は、このリスクとリターンのバランスを適切に取ることを可能にします。
b.多様性の確保
すべての資産が同時に悪いパフォーマンスを示すわけではありません。異なる資産クラスや地域、産業に分散投資することで、特定のリスクを軽減することができます。
c.目標の達成
個々の投資家は異なる目標やリスク許容度を持っています。ポートフォリオ最適化を通じて、これらの目標に沿った最適な投資戦略を策定することが可能です。
d.継続的な再評価
市場環境は絶えず変動します。ポートフォリオ最適化のプロセスは、投資環境の変化に対応し、適切なタイミングでポートフォリオの調整を行うための枠組みを提供します。
最後に、ポートフォリオ最適化は単なる数学的なツールやモデルに過ぎないという認識は避けるべきです。最適化のプロセスは、投資家の目標やビジョンを実現するための手段であり、その背後にある深い洞察や経験に基づいて適用されるべきものです。